Сложные системы и науки о сложности. Краткий обзор
Начиная со второй половины 20 века, большую значимость приобретают науки о сложности, нацеленные на изучение природы и эволюции сложных систем [1]. Термин сложность крайне многогранен, но чаще всего он определен как атрибут некоторого объекта, процесса или явления. Например, мерой колмогоровской сложности выступает длина самого короткого сообщения, необходимого для передачи информации. В теории динамического хаоса для описания природы нелинейных систем используется сложность, определяемая характеристическими показателями Ляпунова. Сложность, описывающая структурные или топографические особенности системы, определяется фрактальными размерностями, конфигурационной энтропией, параметрами порядка. Многие природные объекты и системы, поведение которых внешне воспринимается как хаотическое, объединяет общее свойство – самоподобие или, другими словами, фрактальность, инвариантность относительно изменения масштаба.
Настоящий триумф в этой области произошел в 2021 году, когда трем ученым: Джорджо Паризи (Giorgio Parisi), Клаусу Хассельману (Klaus Hasselmann) и Сюкуро Манабэ (Syukuro Manabe) была вручена Нобелевская премия «…за новаторский вклад в понимание фундаментальной роли флуктуаций и хаоса в эволюции сложных физических систем» [2–4] (Рис. 1).

Рис. 1. Нобелевские лауреты по физике 2021 года
Начиная с 60-х гг. 20 в. С. Манабэ руководил разработкой компьютерных моделей климата Земли, что позволило его научной группе количественно оценить влияние увеличивающейся концентрации углекислого газа в атмосфере на климат. Как показали исследования С. Манабэ увеличение концентрации углекислого газа ведет к росту температуры в нижних слоях земной атмосферы, при этом более высокие слои охлаждаются. Работы ученого заложили основу современного климатического моделирования.
Спустя десятилетие после первых результатов группы С. Манабэ, Клаус Хассельман создает вероятностную модель, в которой смог объединить сложно предсказуемые погодные условия с глобальным климатом. В результате К. Хассельман предлагает методику, позволившую доказать ключевую роль человека в происходящих климатических изменениях. Продолжая работать с этой моделью в дальнейшем, он установил, что различные природные явления, такие как извержения вулканов или изменение солнечной активности, влияют на результаты расчетов характерным образом. Таким образом у каждого явления, включая воздействия в ходе человеческой деятельности, свой «отпечаток пальцев» и, воспроизводя метеорологические наблюдения, можно было понять, какой из факторов больше влиял на тот или иной результат.
Применяя методы статистической физики, Джорджо Паризи в 1980-х гг.20 в. открыл ряд закономерностей в материалах, казавшимися исследователям того времени полностью неупорядоченными, таких как спиновые стекла и разработал математический аппарат для их описания. Его идеи о фундаментальной роли хаоса и флуктуациях в физических системах от атомарных до планетарных масштабов нашли отражение в биологии, нейронауках, машинном обучении и других областях человеческого знания.
В современной литературе под сложными системами понимают составные объекты, представленные значительным числом взаимодействующих компонентов. Подобное взаимодействие приводит к появлению новых эмерджентных свойств сложной системы (сложность, открытость, нелинейность, самоорганизация, адаптивность и др.), например коллективных процессов и явлений, которые не сводятся к простой сумме корреляций между отдельными частями в составе целого. Учет коллективных явлений имеет существенное значение: от физики ускорителей (ограничения интенсивности пучка) и физики конденсированных сред (коллективные эффекты) до коллективного поведения в живой природе. Не следует забывать о необходимости разработки новых методов для изучения свойств отдельных компонентов, входящих в состав целого: эффектов памяти и корреляций, динамических связей, критических переходов и др.
Эволюцию сложных систем достаточно трудно моделировать за счет конкуренции и взаимодействия между компонентами, а также их открытости, т.е. обмена энергией и веществом с окружающей средой. Изучение сложных систем осуществляется в науках о сложности, науках о данных и других междисциплинарных научных направлениях, которые активно развиваются, прежде всего, за счет обмена и распространения научных идей.
На Рис. 2 представлена карта развития наук о сложности, составленная учеными Брайном Кастеллани (Brian Castellani) и Лассе Герритсом (Lasse Gerrits). Кастеллани и Герритс выделяют следующие «интеллектуальные традиции» в науках о сложности: общую теорию систем (системный анализ), теорию сложных систем, теорию динамических систем (теория детерминированного и динамического хаоса, нелинейная динамика), кибернетику и искусственный интеллект. Интерактивная карта позволяет читателям получить информацию о научных направлениях, терминах, ключевых работах, персональных страницах ведущих ученых – создателей научных школ, взаимосвязях научных направлений и идей в виде гиперссылок. Более подробная информация представлена на странице: https://www.art-sciencefactory.com/complexity-map_feb09.html По указанной ссылке можно скачать карту в различных форматах.
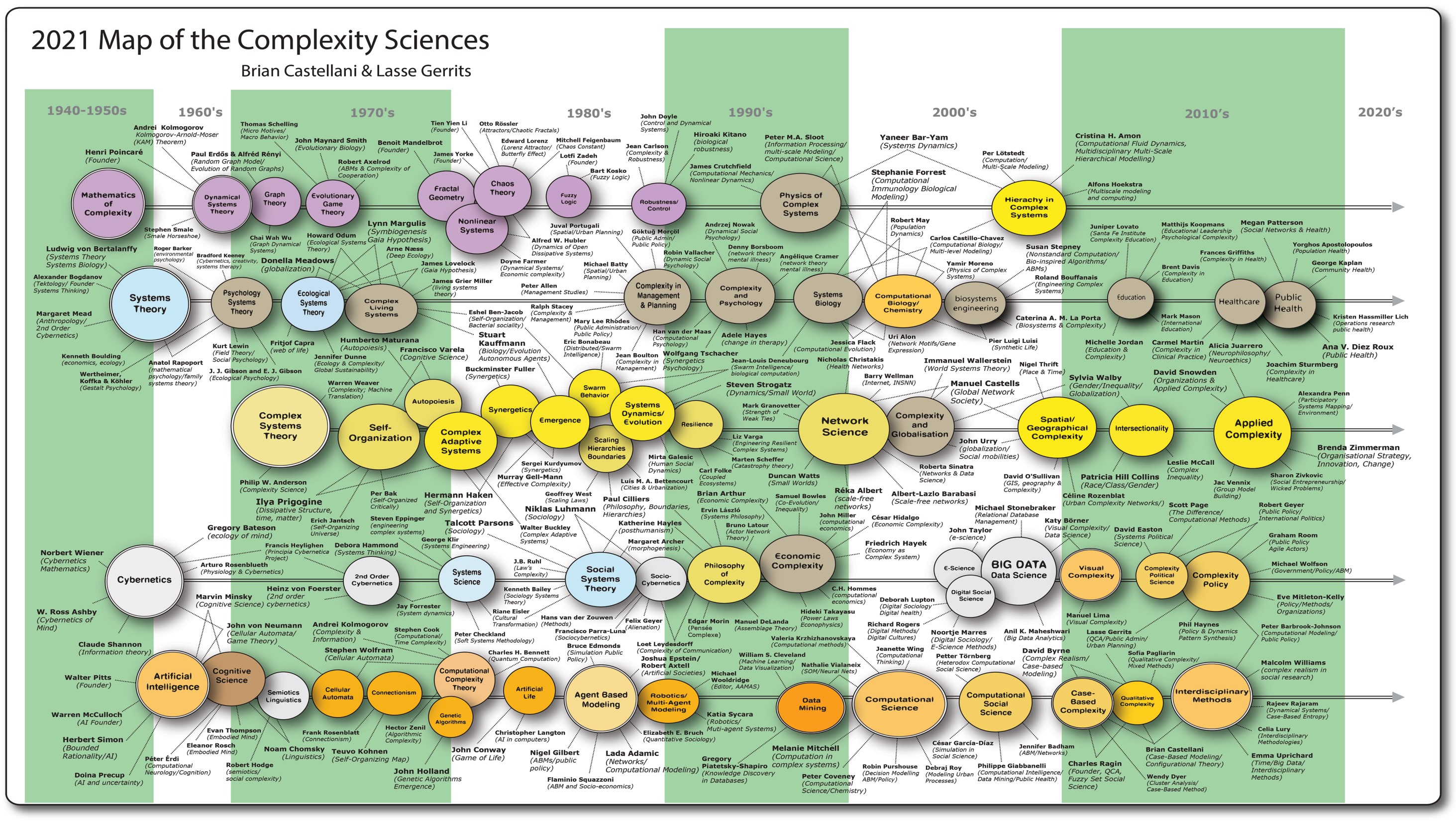
Рис. 2. Эволюция наук о сложности.
В совокупности наук о сложности выделяется физика сложных систем. Главными задачами указанной области являются: применение физических методов в изучении эволюции сложных систем, например статистической физики, а также поиск физических закономерностей при описании поведения и свойств сложных систем.
На кафедре вычислительной физики Казанского федерального университета свыше 20-и лет проводятся исследования уникальных свойств, динамических состояний и эволюции сложных систем разнообразной природы (отдельные результаты в данной области собраны в коллективных монографиях: «Флуктуации и шумы в сложных системах живой и неживой природы». Ред.: Р.М. Юльметьев, А.В. Мокшин, С.А. Демин, М.Х. Салахов, Казань: Министерство образования и науки РТ, 2008, 456 с.; «Динамические явления в сложных системах». Ред.: А.В. Мокшин, С.А. Демин, Р.М. Хуснутдинов, О.Ю. Панищев, Казань: Министерство образования и науки РТ, 2011, 308 с.). Вычислительная физика представляет собой быстро развивающееся научное направление, объединяющее методы и подходы как теоретической, так и экспериментальной физики (Рис. 3).
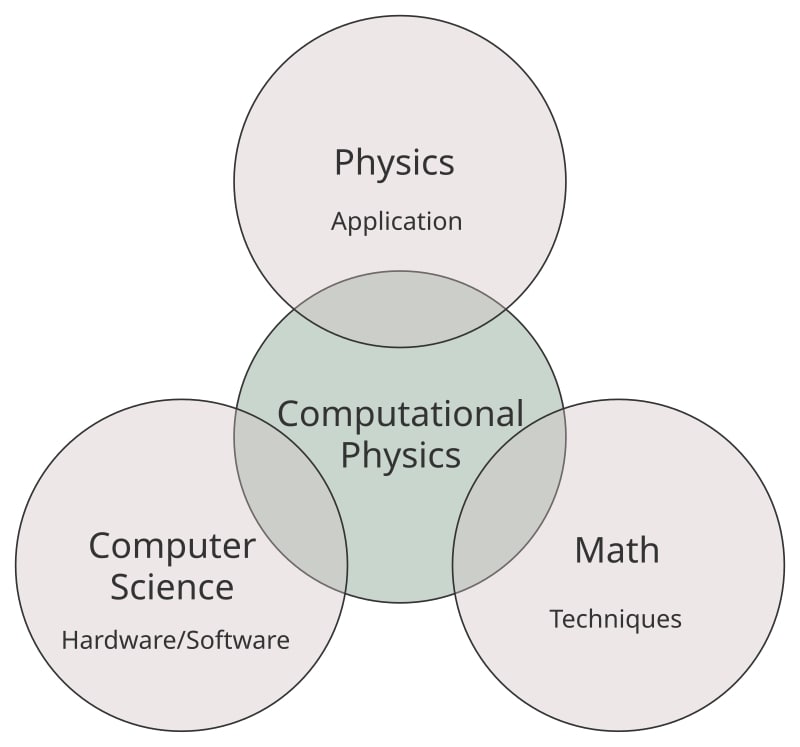
Рис. 3. Вычислительная физика – область, в которой удивительным образом сочетаются как известные теоретические соотношения, так и численные алгоритмы для проведения крупномасштабных компьютерных расчетов.
Для исследования и прогнозирования эволюции сложных систем мы разрабатываем и развиваем как оригинальные теоретические подходы, основанные на фундаментальных идеях неравновесной термодинамики и статистической физики, математической статистики и теории вероятностей, так и методы машинного обучения. При этом совокупность рассматриваемых сложных систем достаточно разнообразна: от физики мозга и живых систем до процессов, распространяющихся в социальных сетях (Рис. 4).
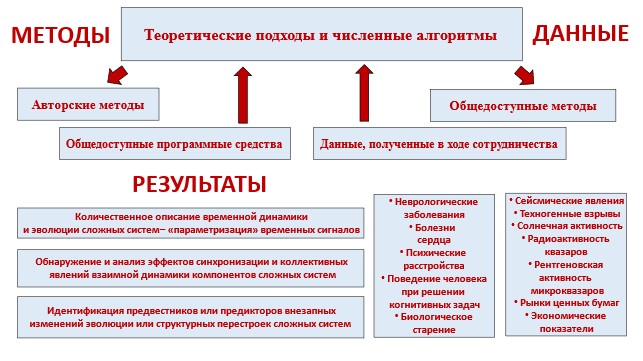
Рис. 4. Исследование сложных систем на кафедре вычислительной физики Казанского университета
Например, в серии научных работ, представленных в ведущих зарубежных и российских журналах, сотрудники кафедры на основе исследования эффектов статистической памяти и корреляций устанавливают диагностические критерии аномального функционирования мозга человека, что проявляется в чрезмерной активности ансамблей нейронов в локальных областях или повышенной согласованности или асинхронности между соседними или дальними областями коры головного мозга [5–8] (Рис. 5). Подробнее с данными результатами можно познакомиться в заключительной части видеолекции «Физика сложных систем: от простого к сложному»(https://www.youtube.com/watch?v=WtEqkXQfqwc&t=232s).
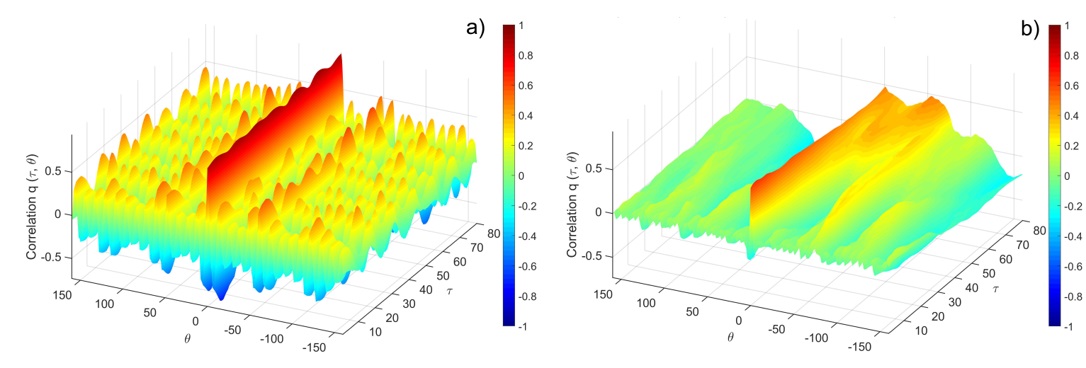
Рис. 5. Разные типы частотно-фазовой синхронизации при нормальной и патологической активности мозга человека
В другом исследовании рассматривается сложная система, поведение которой характеризуется набором различных факторов (внешних или генерируемых самой системой), зависящих от времени. В работе показано, что зависимость этих факторов от времени может быть воспроизведена с помощью нелинейной регрессионной модели, построенной на основе генетических алгоритмов машинного обучения. Модель позволила предсказать возможное поведение системы и выявить значимые факторы, которые оказывают существенное влияние на поведение системы. В качестве примера рассмотрены метеорологические и производственные данные [9].
Значительный интерес вызвала работа сотрудников кафедры, в которой разработана оригинальная методология, характеризующая распространение COVID-19 на произвольной территории[10] (Рис. 6). Созданная методология позволила выявить закономерности в формировании волн коронавируса на территории Российской Федерации. Установлено, что каждая волна коронавирусной инфекции содержит «критический порог». Определение перехода к «взрывному росту» числа заболевших позволит врачам заранее прогнозировать вспышки и эпидемии и принимать меры.С деталями данной работы можно познакомиться на сайте агентства «Аргументы и факты» (https://aif.ru/society/healthcare/volna_za_volnoy_uchyonye_ustanovili_scenariy_rasprostraneniya_kovida_v_rf) или видеосюжете университетского канала UniverTV(https://youtu.be/mIFric8oQU4).
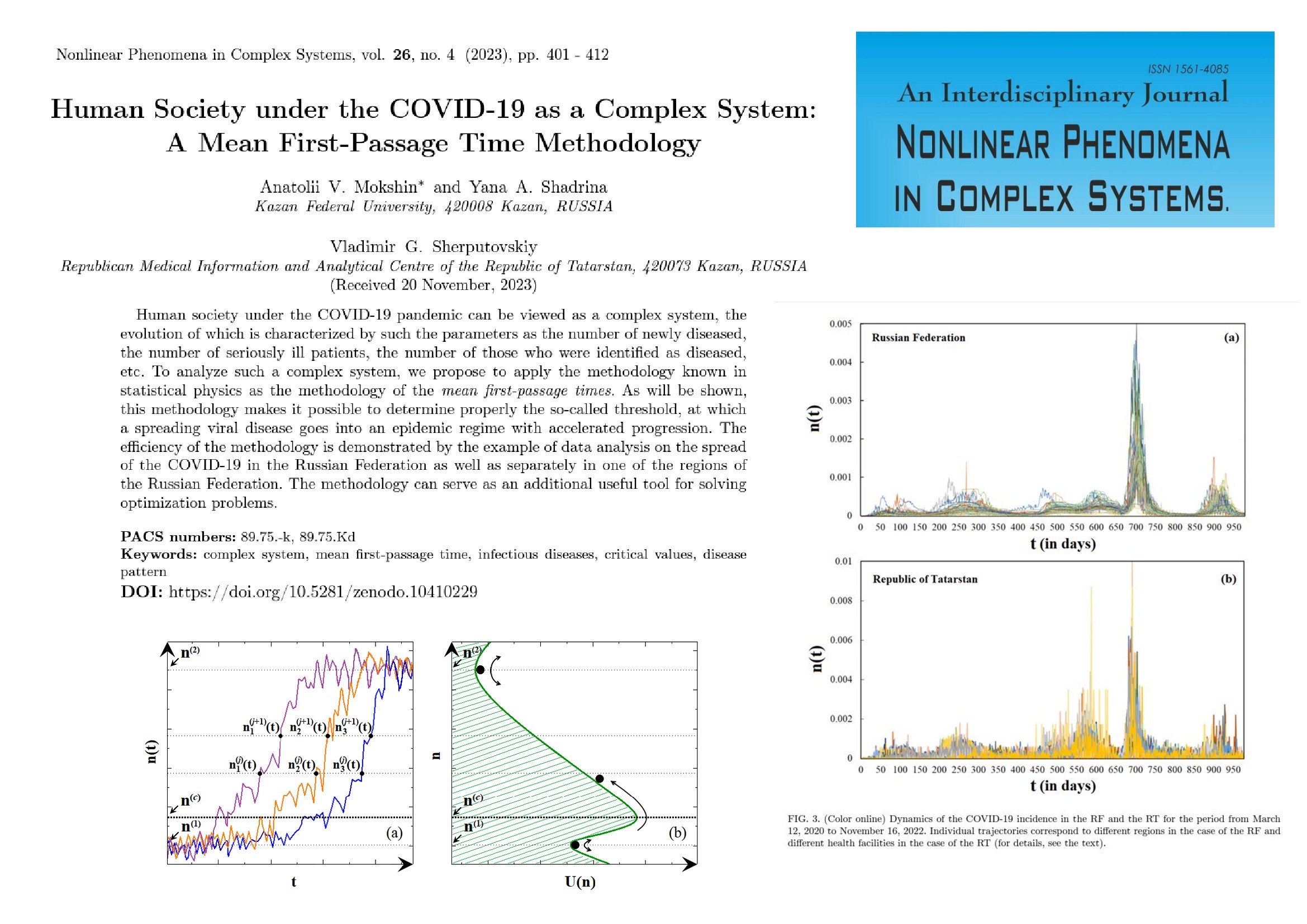
Рис. 6. Исследование особенностей эпидемического процесса COVID-19
С другими научными результатами в области исследования сложных систем можно познакомиться в новостных лентах на страницах кафедры вычислительной физики КФУ в социальных сетях: https://kpfu.ru/physics/struktura/kafedry/kafedra-vychislitelnoj-fiziki и https://vk.com/comp_phys_kpfu
Часть фундаментальных и практических результатов в изучении природы сложных систем была получена совместно со студентами, прикрепленными к кафедре. Проведение научных исследований способствует получению студентами необходимых профессиональных навыков в сфере аналитики данных и IT-индустрии, что в дальнейшем позволяет им устраиваться в ведущие региональные и федеральные организации (https://kpfu.ru/physics/struktura/kafedry/kafedra-vychislitelnoj-fiziki/nashi-vypuskniki).
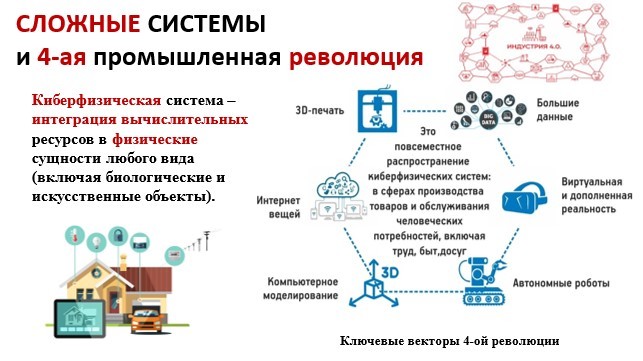
В завершение необходимо отметить, что сочетание методов вычислительной и статистической физики с современными информационными технологиями, например, с алгоритмами машинного обучения позволяет решать прикладные задачи естественных наук новым образом. Полученные результаты способствуют активному развитию современных наук о данных (DataScience, Рис. 7) от анализа и извлечения данных (DataAnalysis – разработка методов и алгоритмов извлечения знаний из экспериментальных данных, DataMining – интеллектуальный анализ данных) до технологий больших данных (BigData– искусственный интеллект, интеллектуальный анализ данных, статистический анализ, моделирование, симуляции). Кроме того, развитие методов вычислительной физики и физики сложных систем становится особенно актуальным в свете существующих приоритетов 4-ой промышленной революции, состоящей в построении, исследовании и прогнозировании поведения киберфизических систем – интеграции вычислительных ресурсов в сложные системы разной сущности (Рис. 8).

Рис. 7. Содержание наук о данных
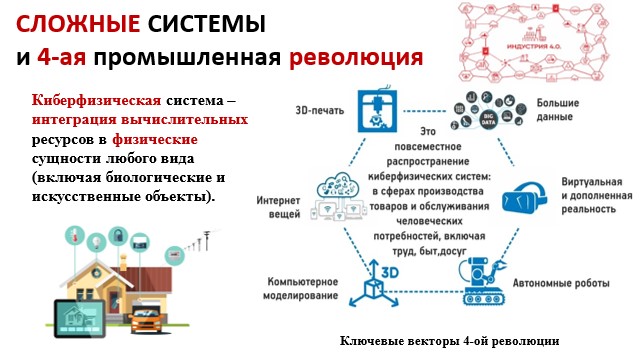
Рис. 8. Сложные системы и Индустрия 4.0
Литература:
1. Weaver W. // Am. Sci. 1948. V. 36. P. 536.
2. Manabe S., Wetherald R.T. // J. Atmos. Sci. 1975. V. 32. P. 3.
3. Hasselmann K. // Clim. Dyn. 1997. V. 13. P. 601.
4. Altarelli G., Parisi G. // Nucl. Phys. B. 1977. V. 126. № 2. P. 298.
5.Panischev O.Y., Demin S.A., Bhattacharya J. // Physica A. 2010. V. 389. P. 4958.
6.Timashev S.F., Panischev O.Y., Polyakov Y.S., Demin S.A., Kaplan A.Y. // Physica A. 2012. V. 391. P. 1179.
7. Demin S., Panischev O., Yunusov V., Timashev S. // Stud. Syst. Decis. Control. 2021. V. 350. P. 27.
8.Yunusov V.A., Demin S.A. // J. Biomed. Photonics Eng. 2023. V. 9(4). P. 040301-1.
9. Mokshin A.V., Mokshin V.V., Sharnin L.M. // Commun. Nonlinear Sci. Numer.2019. V. 71. P. 174.
10. Mokshin A.V., Mokshin V.V., Mirziyarova D.A. // NPCS. 2020. V. 23(3). P. 317.
При подготовке сообщения были использованы материалы сайта www.elementy.ru